Réseau de neurones sans couche cachée

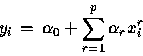
Analogie entre le perceptron multicouches sans couche cachée et la régression linéaire

Le perceptron multicouches sans couche cachée peut être considérer comme une régression linéaire (avec une fonction d'activation linéaire).
Nous allons donc, dans ce paragraphe, comparer la prédictivité d'un tel réseau avec celle de la régression linéaire.

Dans ce cas, le passage des variables d'entrée à la variable de sortie est linéaire. On a donc :

$${\displaystyle y_i\,=\,\alpha_0+\sum_{r=1}^p\alpha_rx_i^r}$$

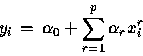
Remarquons que cette équation correspond bien à l'écriture du modèle de régression où :
$\cdot$ y est la variable "réponse"
$\cdot$ $x^1\,,x^2\,\ldots\,x^r$ sont des variables réelles. On veut étudier leur influence sur y.

Comparaison de ces deux méthodes dans notre exemple

$\ast$ Pour le réseau de neurones, on a ici :
$\cdot$ comme variables d'entrée la matrice "temp1[,1:3]"
$\cdot$ comme variable de sortie yy
$\cdot$ pas de variables dans la couche cachée. Donc "size=0"
$\cdot$ une influence directe des variables d'entrée. Donc "skip=T"
$\cdot$ une fonction d'activation linéaire. Donc "linout=T"

D'où la commande Splus suivante :

> rl1_nnet(temp1[,1:3],yy,size=0,decay=0,linout=T,skip=T,maxit=100)

On obtient ainsi les résultats suivants :

# weights:  4
initial  value 1215.329472 
iter  10 value 124.655154
final  value 124.655146 
converged

Ici, 4 est le nombre de paramètres. L'algorithme converge vers la valeur 124.65 qui correspond à la valeur minimale de l'erreur quadratique.

Grâce à la commande "summary", on peut obtenir les poids des différentes connexions qui correspondent en fait à l'estimation des paramètres ${\alpha_r ,\; r\,=\,0,2,\ldots,p}$

> summary(rl1)
a 3-0-1 network with 4 weights
options were - skip-layer connections  linear output units 
  0->4  1->4  2->4  3->4 
  7.69 -0.05  1.12 -0.75

On a ainsi :
$\hat{\alpha}_0 \,=\, 7.69$
$\hat{\alpha}_1 \,=\, -0.05$
$\hat{\alpha}_2 \,=\, 1.12$
$\hat{\alpha}_3 \,=\, -0.75$

$\ast$ Pour la régression linéaire, on a les résultats suivants :

Call: lm(formula = V1 ~ X2 + X3 + X4, data = mat.rl)
Residuals:
    Min     1Q  Median   3Q   Max 
 -4.158 -1.339 -0.5256 1.55 3.862

Coefficients:
              Value Std. Error t value Pr(>|t|) 
(Intercept)  7.6897  5.2681     1.4597  0.1592 
         X2 -0.0519  0.5481    -0.0946  0.9255 
         X3  1.1208  1.9693     0.5691  0.5753 
         X4 -0.7534  1.0825    -0.6960  0.4941 

Residual standard error: 2.436 on 21 degrees of freedom
Multiple R-Squared: 0.05277 
F-statistic: 0.39 on 3 and 21 degrees of freedom, the p-value is 0.7614

On remarque que nous avons les mêmes estimations des paramètres.
A l'aide de la commande "predict" et du résultat de la régression linéaire, on calcule la somme des carrés de l'erreur à savoir :

$${\displaystyle \sum_{i=1}^n(y_i\,-\,\hat{y}_i)^2}$$

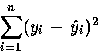
> critere_yy-predict(rl2,mat.rl)
> critere_critere^2
> critere_sum(critere)
[1] 124.6552

On remarque aussi que nous retrouvons le critère à minimiser dans le réseau de neurones.
Conclusion

On a ainsi, par cet exemple, montré que le perceptron multicouches sans couche cachée était équivalent au modèle de régression linéaire.