Soit
-Le Test du Rapport de Vraisemblance est:
![$
\begin{array}{ll}
T_1 & =2[L(y,\widehat{\beta},\widehat{\zeta})-\sup_{\scrip...
...a},\widehat{\zeta})-L(y,\widehat{\beta_0},\widehat{\zeta_0})].\\
\end{array} $](img36.gif)
-Le Test de Wald est:
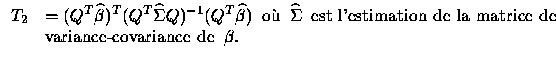
REMARQUE: Le Test de Wald pour
![$T_2=[\frac{\widehat{\beta_j}}{s.e}]^2$](img39.gif) .
.
Quelque soit le test T ci dessus, H0 est rejeté
![]() est la moyenne.
est la moyenne.
![]() Var
Var
![]() est la variance.
est la variance.
![]() L'intervalle de confiance de
L'intervalle de confiance de ![]() ,
de sécurité approximative
,
de sécurité approximative
![]() ,
est
,
est
![]() où l est le
où l est le
![]() quantile de N(0,1) et s.e est l'erreur standard de
quantile de N(0,1) et s.e est l'erreur standard de
![]() .
.
![]() Les Tests:
Les Tests:
Soit
![]() avec Q matrice q*p de rang q.
avec Q matrice q*p de rang q.
-Le Test du Rapport de Vraisemblance est:
![$
\begin{array}{ll}
T_1 & =2[L(y,\widehat{\beta},\widehat{\zeta})-\sup_{\scrip...
...a},\widehat{\zeta})-L(y,\widehat{\beta_0},\widehat{\zeta_0})].\\
\end{array} $](img36.gif)
-Le Test de Wald est:
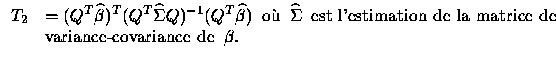
REMARQUE: Le Test de Wald pour
![]()
![]() + est
+ est
![$T_2=[\frac{\widehat{\beta_j}}{s.e}]^2$](img39.gif) .
.
Quelque soit le test T ci dessus, H0 est rejeté
![]() quantile de la distribution
quantile de la distribution ![]() .
.