



Next: Propriétés
Up: Les Modèles Linéaires Généralisés
Previous: Les Modèles Linéaires Généralisés
 Un modèle linéaire généralisé est la donnée des observations
y1,...,yn de n variables aléatoires réelles
Y1,...,Yn
indépendantes et de densités respectives :
Un modèle linéaire généralisé est la donnée des observations
y1,...,yn de n variables aléatoires réelles
Y1,...,Yn
indépendantes et de densités respectives :
Avec:
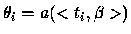
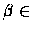
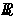 p et
p et 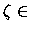
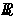 + inconnus
+ inconnus
ti,a,b,c applications connues
a injective
a et b possédant des dérivées secondes
U indépendant de 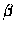 et de
et de 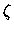 .
.
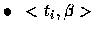 est le prédicteur linéaire pour l'observation yi.
est le prédicteur linéaire pour l'observation yi.
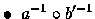 est la fonction de lien l.
est la fonction de lien l.
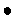 Si a=Id alors l=b'-1 est la fonction de lien canonique.
Si a=Id alors l=b'-1 est la fonction de lien canonique.
 est la fonction variance.
est la fonction variance.
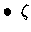 est le paramètre d'échelle.
est le paramètre d'échelle.
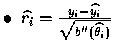 est le résidu de
Pearson (avec
est le résidu de
Pearson (avec
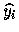 l'estimation de yi et
l'estimation de yi et
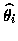 celle de
celle de 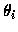 ).
).
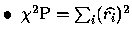 est le
est le 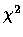 de Pearson.
de Pearson.
 Etant donné un Modèle Linéaire Généralisé défini comme précédement, on lui
associe le modèle saturé défini par:
Etant donné un Modèle Linéaire Généralisé défini comme précédement, on lui
associe le modèle saturé défini par:
Y1,...,Yn sont indépendants.
Yi a pour densité:
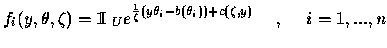 .
.
Le paramètre inconnu est donc
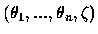 .
.
La Log-vraisemblance du modèle saturé est donc:
![$L(y,\theta,\zeta)=\frac{1}{\zeta}\sum_i[y_i\theta_i-b(\theta_i)]+\sum_ic(\zeta,y_i)$](img22.gif) .
.
L'estimation de 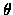 par le maximum de vraisemblance est
par le maximum de vraisemblance est
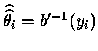 .
.
De plus, on pose
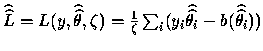 .
.
Etant donné donc un Modèle Linéaire Généralisé avec 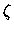 inconnu, on appelle déviance du modèle:
inconnu, on appelle déviance du modèle:
Dev
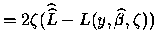 .
.
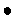 Si
Si 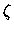 est connu, la déviance normée (scaled déviance) est:
est connu, la déviance normée (scaled déviance) est:
S.Dev
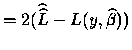 .
.




Next: Propriétés
Up: Les Modèles Linéaires Généralisés
Previous: Les Modèles Linéaires Généralisés
Joseph Saint Pierre
1998-12-10
![]() Un modèle linéaire généralisé est la donnée des observations
y1,...,yn de n variables aléatoires réelles
Y1,...,Yn
indépendantes et de densités respectives :
Un modèle linéaire généralisé est la donnée des observations
y1,...,yn de n variables aléatoires réelles
Y1,...,Yn
indépendantes et de densités respectives :
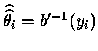 .
.
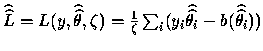 .
.
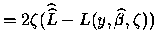 .
.
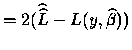 .
.